吴恩达机器学习-Day_5

6.1分类

　　　是/否，可以有两个取值的变量
　　　$$y\in\left\{0,1\right\}$$
　　　0: 负类”Negative Class”(e.g., benign tumor)
　　　1: 正类”Positive Class”(e.g., malignant tumor)
　　　如果y取值多的叫多分类

　　　
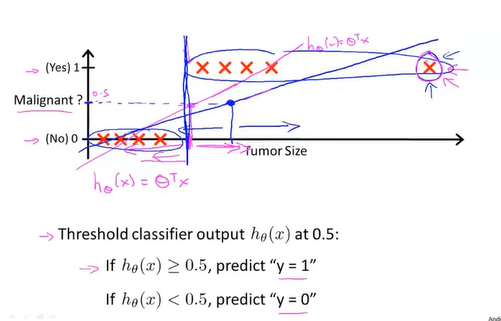
　　　如果和线性回归一样设假设函数，设置阈值为0.5，即如果假设函数值等于阈值时，对应的横坐标左侧的函数值都视为0，反之视为1.
　　　但是这种方法在有极端数据之后，假设函数在图像上的斜率变小，从而当函数值等于阈值时，有很多呈阳性的肿瘤被判断成阴性（在阈值对应的横坐标的左侧），从而造成错误的预测。所以线性回归不适合运用在分类问题。
　　　而且使用线性回归时，假设函数值可能会远大于1或者远小于0，这显得很奇怪。
　　　（个人感觉并不奇怪，因为有设定一个阈值，关键问题在于线性回归会受到偏于优势的数据的影响，类如上面那个例子，设肿瘤体积小于2为分类标准，如果数据点集中在小于2的部分，则会斜率增加，把原本属于阴性的误判为阳性的，同理对阳性也是如此）

　　　逻辑回归Logistic Regression可以保证加黑色函数值能够保持在[0,1]

6-2假设陈述

　　　原来的线性回归方程假设为$h_\theta\left(x\right) = \theta^Tx$
那么逻辑方程就令$$h_\theta\left(x\right) = g(\theta^Tx)$$
$$g(z) = \frac{1}{1+e^{-z}}$$
　　　Sigmoid function = Logistic function都指代g函数
$$h_\theta\left(x\right) = \frac{1}{1+e^{-\theta^Tx}}$$
　　　
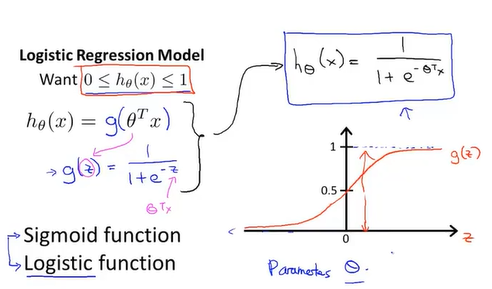
　　　假设函数的图像大约如上图所示。

　　　在逻辑回归方程里的假设函数$h_\theta\left(x\right)$表示估计当x取某值时y=1的概率。
　　　即概率论里的条件概率，也可以写为$P\left(y=0|x;\theta\right)$

6-3决策界限

线性决策界限

　　　
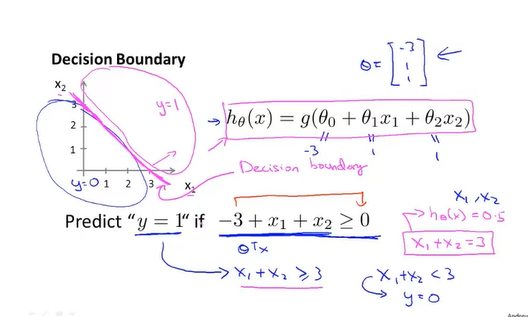
　　　决策界限decision boundary: 假设函数对应的直线，按照其函数值小于/大于阈值将图像分成两个部分就像分界线一样(如图中红色线)。
　　　决策界限不是训练集的属性，而是假设函数的属性。

非线性决策界限

　　　
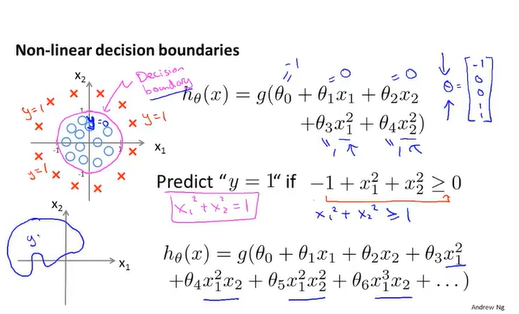
　　　其实就像回归方程，除了要找出合适的参数theta，还要找到合适的多项式方程。

6-4代价函数

　　　
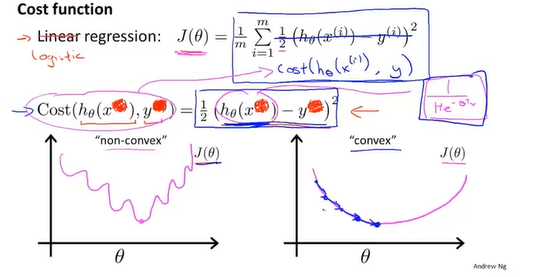
　　　在logicstic回归的代价函数和线性回归的代价函数不同，原因在于逻辑回归的假设函数时非线性的，会导致代价函数有多个局部最小值。
　　　在逻辑回归的代价函数将被写为
$$J\left(\theta\right)=\frac{1}{m}\sum_{i=1}^{m}{Cost\left(h_\theta\left(x\right),y\right)}$$
　　　
　　　
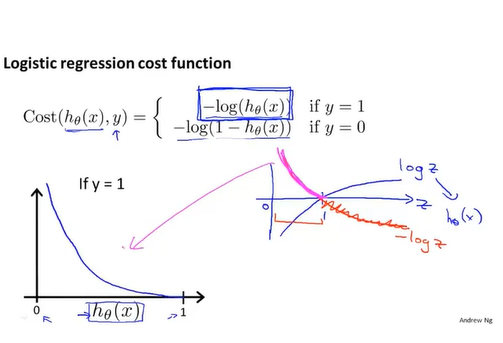
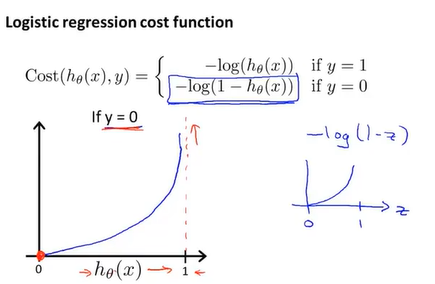
　　　对y=1来说，如果假设函数值为1，那么cost为0，而假设函数越趋于0，则代价越高，即如果我们计算得到假设函数值为0，而y却为1，则我们用一个很大的代价”惩罚”这个学习算法。

6-5简化代价函数和梯度下降

　　　上面提到的代价函数需要分为y=0和y=1的情况，但是可以再简化为
　　　
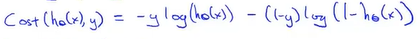
　　　似乎可以采用其它代价函数，但是这种形式是从极大似然法maximum likelihood estimation得来的。
　　　

6-6高级优化

　　　优化算法：Conjugate gradient, BFGS, L-BFGS
　　　优点：不需要认为选择学习率，算法内部的智能内循环(线搜索算法);常常快于梯度下降算法。
　　　缺点：太复杂。
　　　

6-7多元分类：一对多

　　　
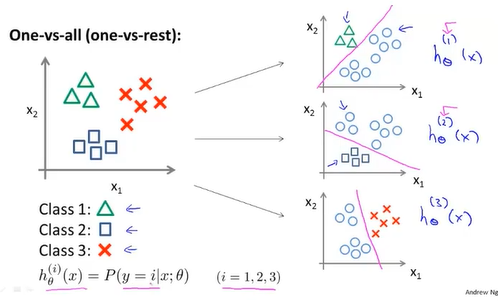
　　　需要n个分类器来分出n个种类，每个分类器可以分出代价最小的种群。（有个疑问：会不会有某个或多个样本同时处在多个类中？）