吴恩达机器学习-Day_6

7-1过拟合问题

　　　过拟合问题the overfitting problem: 函数模型符合已知数据点但无法用于处理未知问题，简单说就是有特殊性但是没有普遍性。
　　　正则化regularizatoin: 改善和减少过度拟合。

过拟合问题

　　　
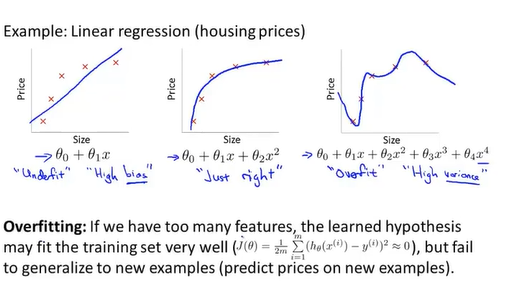
　　　左边: 欠拟合underfit, 高偏差high bias.
　　　右边：过拟合overfit, 高方差high Variance.
　　　泛化generalize: 对一般化的数据也同样适用。
　　　

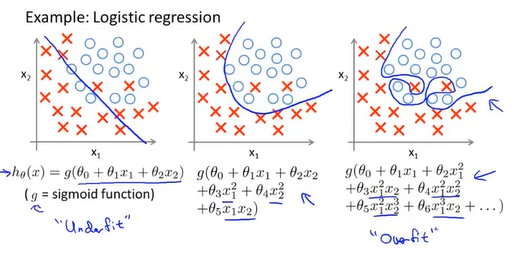
优化方法

　　　1.减少特征数量
　　　　　　-人工选择重要的特征
　　　　　　-模型选择算法(后面提到)
　　　2.正则化
　　　　　　-保留所有的特征，但减少量级magnitude或者参数theta的大小
　　　　　　-在有很多特征的情况下工作较好，每个特征会为预测y提供一点帮助。

7-2代价函数

　　　
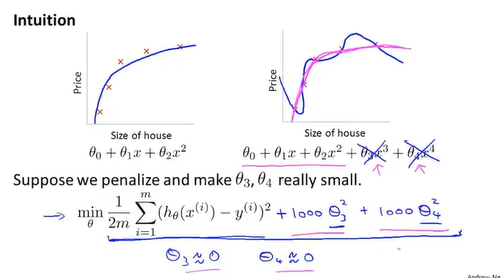
　　　对部分参数加入惩罚项，在图中所示，给后面两个参数增加惩罚项减少其对假设函数的影响，使函数更趋近于二次函数。

　　正规化:
　　　减少参数theta的值
　　　　　　-简化假设函数
　　　　　　-防止发生过拟合
　　　在代价函数加入惩罚项
　　　
　　　代价函数 $$J\left(\theta\right) = \frac{1}{2m} \left[\sum_{i=1}^m{\left(h_\theta\left(x^{\left(i\right)}\right)-y^{\left(i\right)}\right)}^2 +\lambda \sum_{j=1}^n{\theta_j^2}\right]$$
　　　注意后面的惩罚项是从j=1开始，不包含$\theta_0$。其中$\lambda$叫做正规化系数，如果正规化系数过大会导致”惩罚”过重，最后假设函数收敛到一条和x轴平行的直线y = $\theta_0$。

7-3线性回归的正则化

　　　梯度下降
$$ θ_0 := θ_0 - \alpha \frac{1}{m} \sum_{i=1}^m{\left(h_θ\left(x^{i}\right)-y\right)}x_0^{\left(i\right)} $$
$$θ_j := θ_j - \alpha \frac{1}{m} \sum_{i=1}^m{\left(h_θ\left(x^{i}\right)-y\right)}x^{\left(i\right)} + \frac{\lambda}{m}\theta_j$$
　　　上面的式子也可以写成
$$θ_j := θ_j\left(1-\alpha\frac{\lambda}{m}\right) - \alpha \frac{1}{m} \sum_{i=1}^m{\left(h_θ\left(x^{i}\right)-y\right)}x^{\left(i\right)}$$
　　　其中由于$\alpha$的值很小，所以$θ_j\left(1-\alpha\frac{\lambda}{m}\right)$的值解仅1。
　　　
　　　如果样本数小于特征数，则会导致矩阵退化（即不可逆矩阵）
　　　PS: 这个方程使用过代价函数对theta求导后结果为0推出。

7-4逻辑回归的正则化

　　　加入正则化项的逻辑回归模型的代价函数
　　　
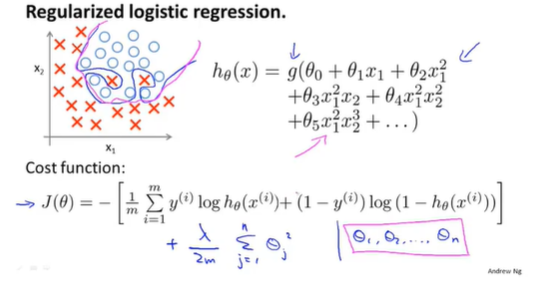
　　　代价函数即为原来的代价函数加上正则化项$\frac{\lambda}{2m}\sum_{j=1}^n{\theta_j^2}$
　　　加入正则化项的逻辑回归模型的梯度下降
　　　
　　　弹幕里有人提到为什么后面的theta不用累加的问题，因为每次都是对$theta_j$求偏导，其它下标不是j的在求导的时候就变成0了，所以不是和代价函数一样求和。

高级优化

　　　
　　　这节课后面再coursera有个练习==，有时间再做吧

8-1非线性假设

　　　
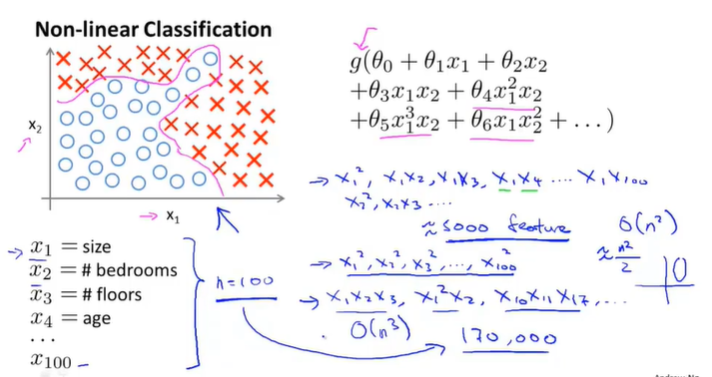
　　　如果特征数量过多，便会导致产生的多项式项数过多，会发生过拟合，但是如果通过减少次数来减少项数又会减少相关项导致曲线欠拟合。
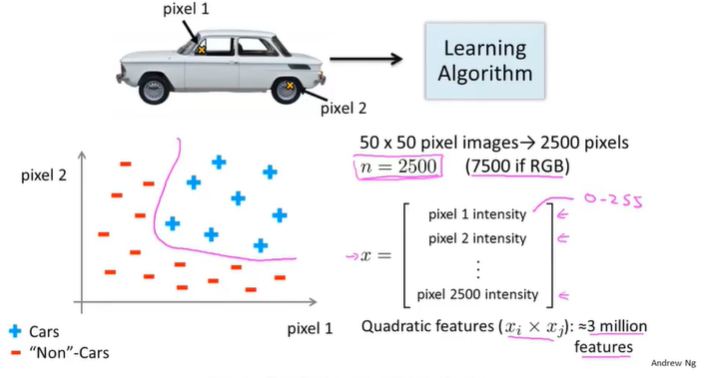
　　　由于计算机看到的只是代表亮度的矩阵，那么为了使计算机有识别能力，需要向学习算法提供车和非车的样本集，以下是原理示例。
　　　在车上取某两个位置的像素点，根据亮度值标注在图上，车和非车也同样如此处理，如下图所示：
　　　

8-2神经元和大脑

　　　神经网络neural networks起源: 尝试去模拟人的大脑的算法。
　　　盛行于80年代和90年代早期，但是没落与90年代末，由于计算速度提高在近阶段兴盛。
　　　生理学上的证据：切断耳朵和大脑上听觉中枢的神经，接上眼睛后这个大脑区域拥有看的能力。（神经重连实验）

8-3模型展示

　　　人类是通过神经元进行信息传递。
　　　所以在计算机里面，神经网络将逻辑单元当做神经元。
　　　Sigmoid(logistic) 激活函数actication funciont。
　　　theta参数在某些文献里面也会被叫做权重weight
　　　可能会有偏置单元bias unit.
　　　在神经网络中，第一层也叫作输入层input layer,最后一层叫做输出层output layer, 中间的叫做隐藏层hidden layer.
　　　
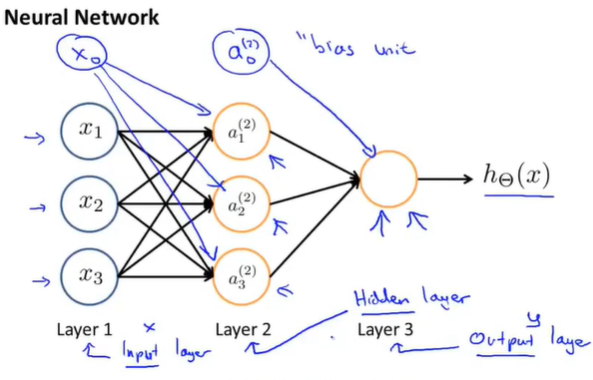
　　　$a_i^{\left(j\right)}$=第j层的第i个激活项
　　　$\theta^{\left(j\right)}$=权重矩阵控制从j层到j+1等的映射函数。