吴恩达机器学习Day7

8-4模型展示

　　　前向传播Forward propagation的神经网络。方程的向量化表示。
　　　
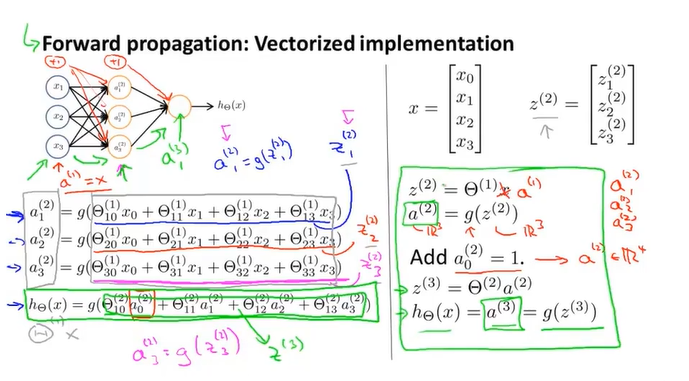
　　　注意这里的$z^{\left(2\right)}=\Theta^{\left(1\right)}a^{\left(1\right)}$ 是把x也看成了a，然后在计算之后需要给各个层加偏置项，即下标为0的那一项。

　　　
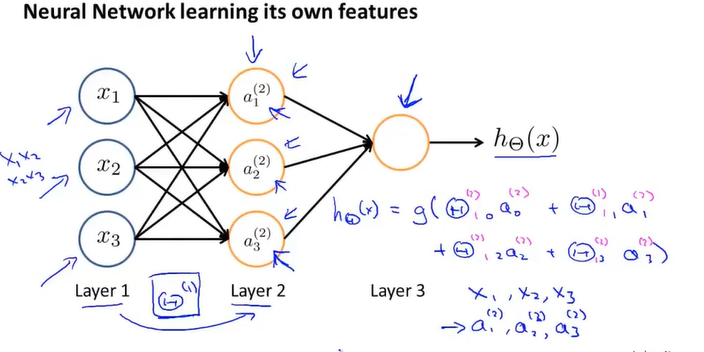
　　　这一步是从隐藏层推出输出层，这一步和逻辑回归的假设函数相似，这不过区别在于标记Theta，且输入的特征是来自于隐藏层，而不是原本数据的特征。
　　　即没有使用样本的特征，而是用训练出来的逻辑回归的结果作为特征。

　　　其它的神经网络的结构，不止上面的三层结构，可能有多个隐藏层。

8-5例子和直觉理解

　　　
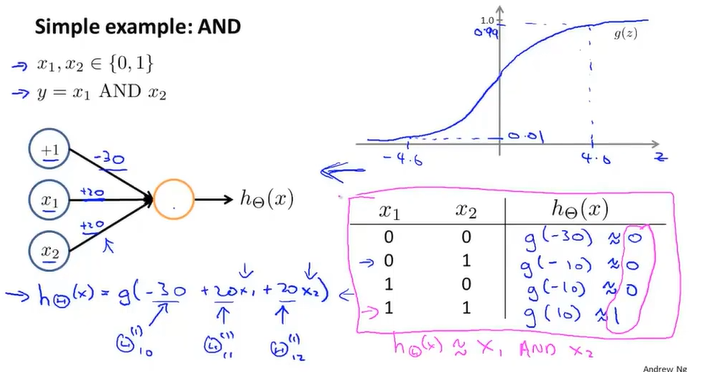
　　　神经网络运用在与门上，加入一个偏置单元。Theta的值是由教授本身提供。g(4.6)的值接近0.99
　　　这些例子只有两层，还是算比较入门的神经网络

8-6例子和直觉理解

　　　
　　　神经网络算出非门的假设函数

　　　加下来是比较复杂的
　　　
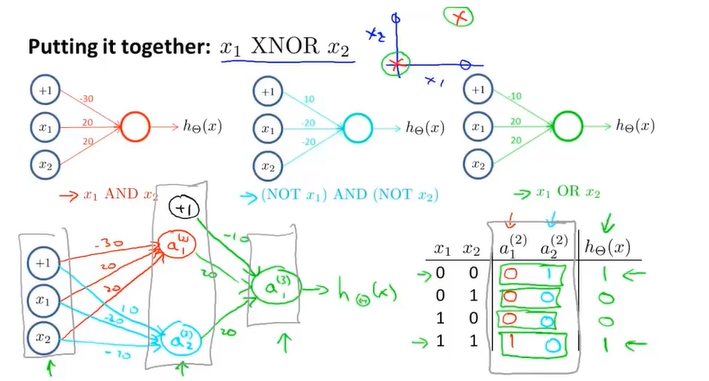
　　　这一步相当于 $(x_1 AND x_2) OR (NOT x_1 AND NOT x_2) = x_1 XNOR x_2$
　　　有点像逻辑的相互叠加。

8-7多元分类

9-1代价函数

　　　
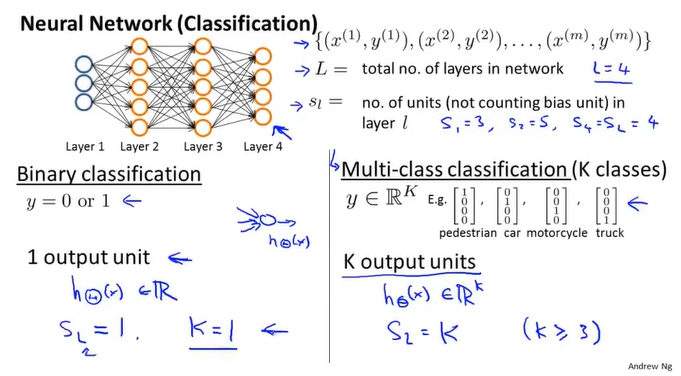
　　　L: 在神经网络里层次数量
　　　$s_l$: 在层次l里有几个单元
　　　
　　　神经网络的代价函数: K是指最后y有几个输入，如[0 0 1 0]`这种的就有4种输出，至于在正规化项中的求和，$s_l+1$是加上偏置项+1的结果；因为每个单元之间相连，所以有$s_l+1*s_l$种链接方式，除去输出层后，总共是L-1层。

9-2反向传播算法

　　　反向传播算法Back propagation
　　　
　　　
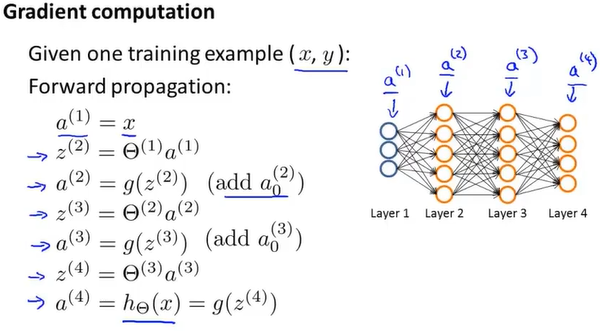
　　　这边的梯度我也没看懂怎么推的，省略太多步了，后面有时间再来看看吧。
　　　
　　　先用正向传播来求出每一层的激活项a，然后你用反向传播求出每一层的$\delta$，$\Delta$累加上激活项和$\delta$的乘积，加上正则化项之后才是正规化的梯度下降D。这一节的公式挺好理解，但是原理和数学推导看着一脸懵。

9-3理解反向传播

前向传播

　　　
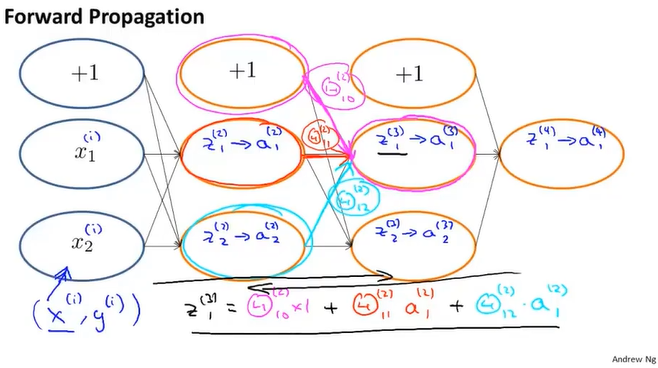
　　　这个前向传播和前面的与或门类似。

反向传播

　　　
　　　这里忽略了正则化项，且把代价函数近似的看作(h(x)-y)的平方。
　　　
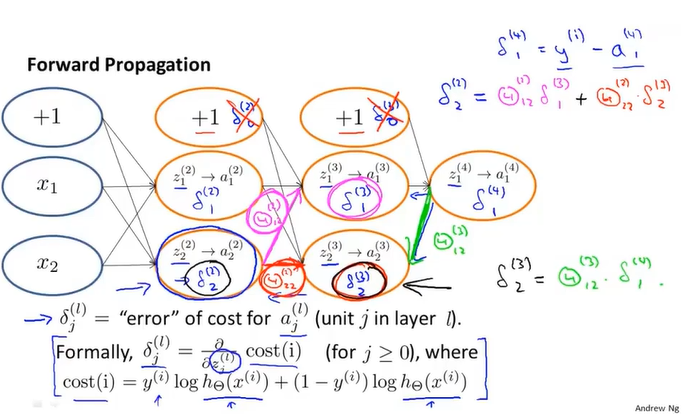
　　　怎么感觉有点像递归啊……前面讲的delta计算公式和这边写的不一样，应该是因为前面的激活项乘上系数theta之后变换变成了这一边的delta。

9-4使用注意：展开参数

　　　如何把参数从矩阵变成向量
　　　
　　　这里我觉得只有三层，应该是只有2个theta……，所以我觉得应该是没有存在theta2，或者theta1.
　　　将向量化后的矩阵输入到代价函数中，然后再在函数体内reshape成矩阵。

9-5梯度检测

　　　Gradient Checking，在反向传播中可能会出现bug产生误差，需要梯度检测，以下是原理和实现方式。
　　　
　　　
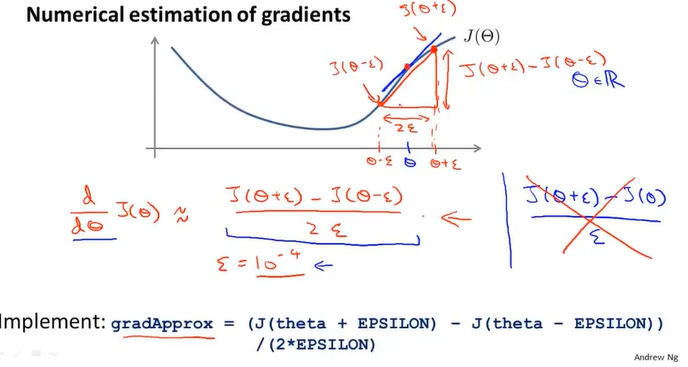
　　　实现的代码
　　　

　　　整个过程步骤如下：
　　　　　　用反向传播计算DVec
　　　　　　使用梯度下降检测
　　　　　　确定两者的值相似
　　　　　　关闭梯度检测，使用反向传播的代码去学习，因为梯度检测的代码太慢

9-6随机初始化

　　　这里初始化的是Theta
　　　在神经网络里面将Theta设置为0是没有意义的，因为同一层次的各个单元在梯度下降中的值都会一样，这是高度冗余的。
　　　所以Theta中的值会被随机化为[-epsilon,epsilon]之间的数。

9-7组合到一起

　　　最常用的是使用一个隐藏层。多个隐藏层的话需要每个隐藏层的隐藏单元数要相等，正常是输入特征数的1-3倍。隐藏单元数越多越好，但是会加大计算量。
　　　步骤：
　　　　　　1.随机初始化权重Theta
　　　　　　2.使用正向传播计算假设函数的值（激活项）
　　　　　　3.计算代价函数
　　　　　　4.使用反向传播计算偏导数
　　　　　　5.使用梯度检查检测已经得到的偏导数项
　　　　　　6.使用梯度下降或者高级优化方法结合反向传递去最小化以Theta为参数的代价函数

9-8无人驾驶

　　　视频……92年的无人驾驶技术。。

10-1决定下一步做什么

　　　改正一个学习算法的方法
　　　　　　-获得更多的训练样本
　　　　　　-使用更小的特征集
　　　　　　-使用额外的特征
　　　　　　-尝试加入高级幂的特征
　　　　　　-选取合适的lambda
　　　机器学习诊断Machine learning diagnostic
　　　　　　检查一个学习算法的运行效果，从而获得指导更好知道如何提高算法的效果。