吴恩达机器学习day_9

10-2评估假设

　　　随机分布后按照7：3把数据集分别分成训练集和测试集
　　　在训练集中计算参数theta
　　　计算测试集误差
　　　得到非分类误差Misclassfication error,即测试集代价函数值大于阈值，可是最后实际结果却归为1.

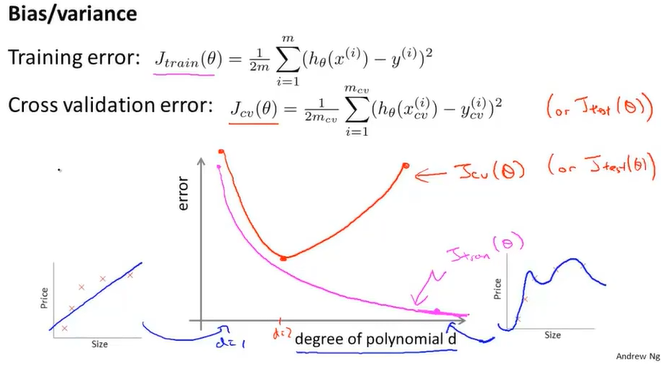
10-3模型选择和训练、验证测试集

模型选择

　　　设置参数d表示级数，d=1表示最高次数为1.
　　　通过每一个不同的d学习出不同的theta，再计算该级数下算出的theta的代价函数值。但是拟合后的最优模型可能是对测试集表现较好，但是对新样本表现可能不一定很好。
　　　 解决方法
　　　　　　-将样本分为6：2：2，分别为训练集、交叉偏差集cv和测试集
　　　
　　　和之前不同的是，这边用的是交叉测试集去测试参数d选出合适的次数，再用这个d去你和参数。

　　　使用测试集选出模型，再用同一个测试集拟合参数不是一个好主意。

10-4诊断偏差和方差

　　　
　　　
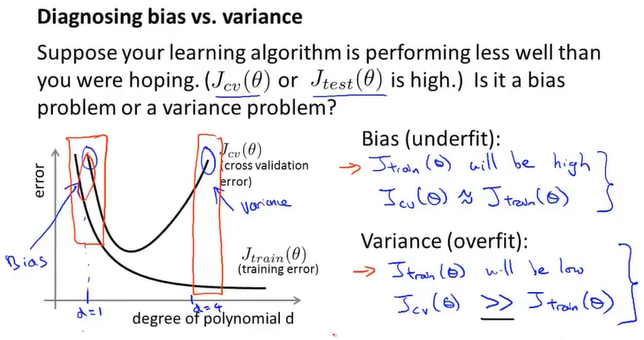
　　　　　　如果训练误差和交叉误差都很大，说明是高偏差的欠拟合
　　　　　　如果训练误差小而交叉误差大，说明是高方差的过拟合

10-5正则化的偏差和误差

　　　找出合适的lambda值
　　　　　　这里使用的是翻倍去计算
　　　
　　　

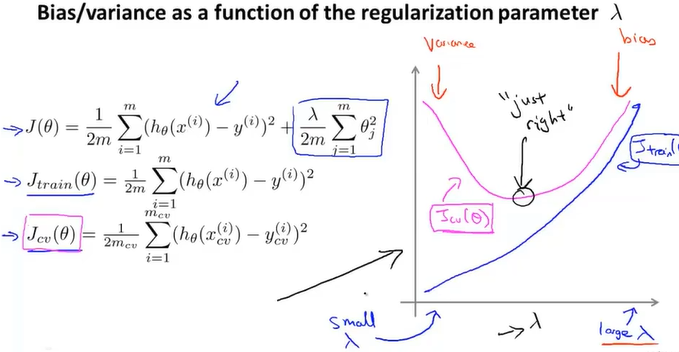
10-6学习曲线

正常情况

　　　
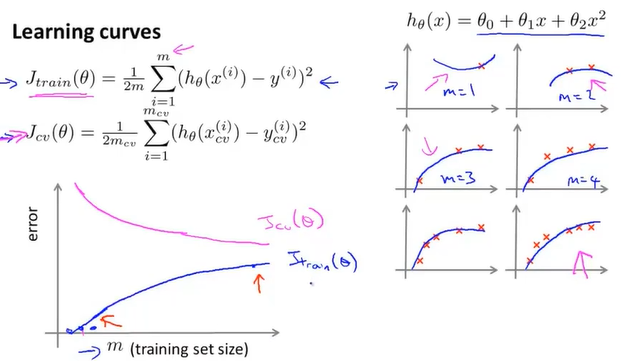
　　　　　　这里的误差是平均误差, 且训练误差最后接近训练集的误差

高偏差

　　　
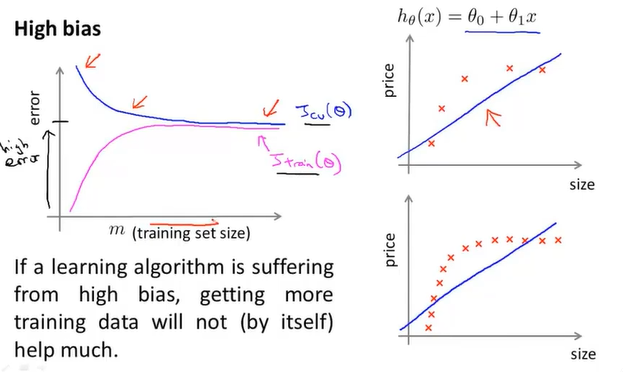
　　　　　　训练误差最后接近交叉集的误差，不过误差都较高，且更快趋于平缓.即在此之后不管如何增加训练集规模效果都不会增加

高方差

　　　
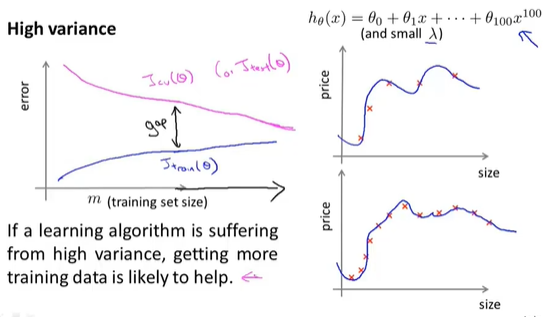
　　　　　　增加更多数据到训练集可以提高算法效果

10-7决定接下来做什么

　　　- 获得更多的训练集 ——解决高方差
　　　- 尝试更小的特征 ——解决高方差
　　　- 尝试增加额外的特征 ——解决高误差
　　　- 尝试增加高级幂的特征 ——解决高误差
　　　- 尝试减少正则化系数lambda ——解决高误差
　　　- 尝试增加正则化系数lambda ——解决高方差
　　　

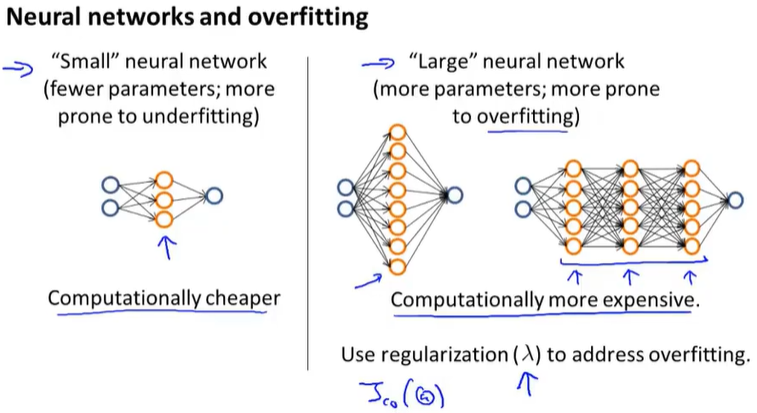
11-1决定执行的优先级

　　　例如在邮件分类器里。
　　　这里模型的特征是关键词，出现关键词则为1，否则为0.
　　　如何减少误差
　　　　　　- 收集更多的数据
　　　　　　- 基于邮件来源（邮件标题）使用更加复杂的特征　　　　　　- 基于邮件信息（邮件主体）使用更加复杂的特征（如discount和discounts）
　　　　　　- 基于识别错拼字使用更加复杂的算法

11-2误差分析

　　　- 从一个简单实现的算法开始，在验证集上应用并测试。
　　　- 画出学习曲线决定是否需要更多的数据和特征
　　　- 误差分析: 人为测试被错误分类的误差，从而寻找能否选出更加系统的特征或更好的修正方法。

数值计算的重要性

　　　如词干提取stemming, 邮件分类是否需要词干提取，取决于使用这种方法能否有效提高分类正确率。
　　　从数学的角度上，最好使用验证集来进行误差分析。

11-3不对称性分类的误差评估

　　　偏斜类skewed classes: 正和负的比例处于极端的情况
　　　对偏斜类进行误差分析无法评价算法效能

　　　查准率Precision: 在预测值为1的情况下有多少真正值为1.
　　　召回率Recall: 在真正值为1的情况下有多少预测值为1
　　　

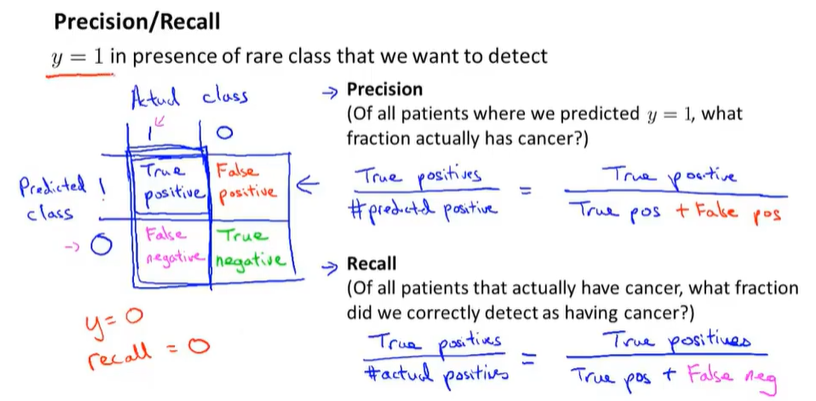
11-4查准率和召回率的权衡

　　　修改阈值，如果阈值提高，则会增加查准率，但是会降低召回率。反之，则会减少查准率，提高召回率。

如何从查准率和召回率抉择不同算法

　　　设P为查准率，R为召回率，用算数平均值$\frac{P+R}{2}$并不是一个很好的方法
　　　$F_1Score:2\frac{PR}{P+R}$
　　　用F值可以避免选到P或者R取到极端小值的情况。

11-5机器学习数据

　　　- 大量的数据量才能体现出好的算法的优势
　　　- 合适的特征能够帮助更好的预测
　　　- 使用多个特征减少偏差，训练集数量大于特征量能够有效解决高方差带来的过拟合。

12-1优化目标

　　　支持向量机the Support Vector Machine, SVM.
　　　
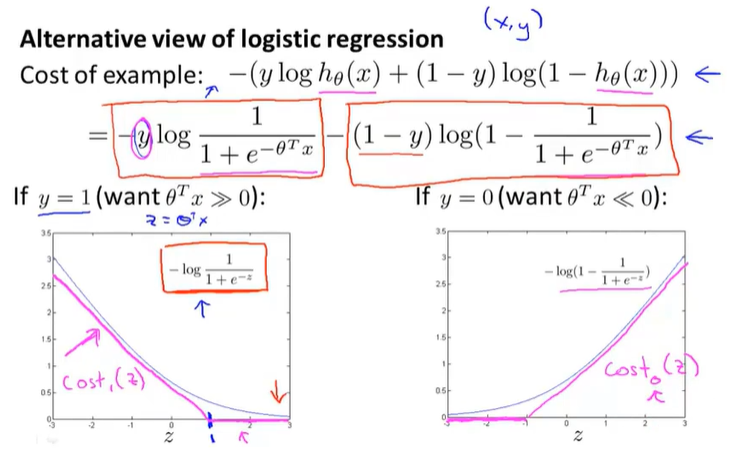
　　　用两条线来替代逻辑回归的函数图像
　　　
　　　支持向量机公式的来源
　　　如果X*theta>=0， 则预测为1，否则预测为0

12-2直观上对大间隔的理解

SVM的决策边界

　　　
　　　
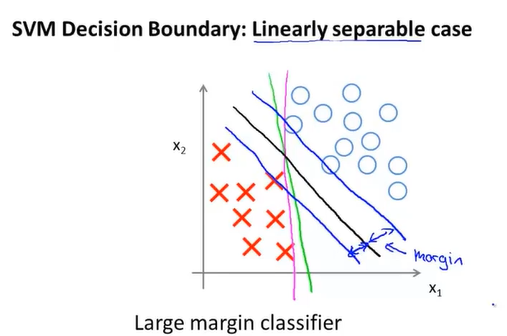
　　　例如线性可分，如果假设C是一个很大的数时，支持向量机会选择距离两种样本集间距margin最大的决策边界。
　　　
　　　上面提到C足够大的话，会按照两个样本集之间的最大间距去区分，但是如果出现了异常数据的话会过于敏感，像上图由于出现了一场样本，原本较为正确的黑线被调整为粉线。所以C要取到适合的值。