吴恩达机器学习-Day_10

12-3大间距分类器的数学原理

　　　向量的内积
　　　范数norm(||$\vec m$||):向量的长度
　　　
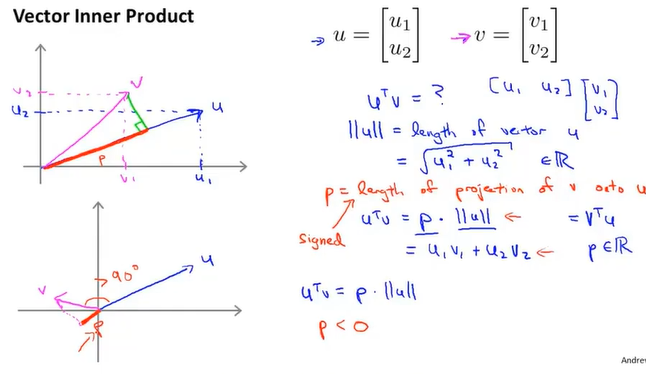
　　　即两个向量的内积等于u的范数乘上p在向量方向上的投影
　　　
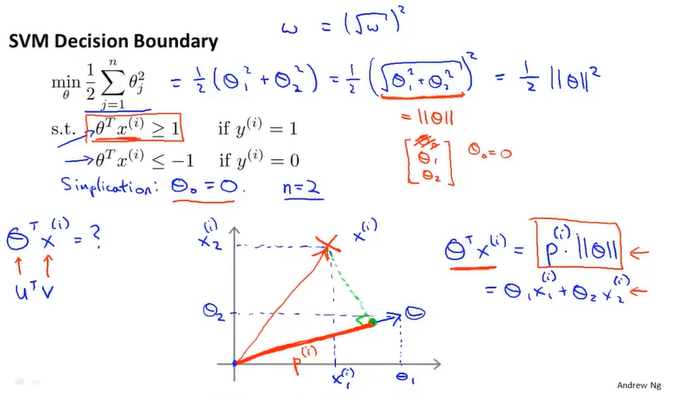
　　　类似上面的内容将$\theta^TX化成p · ||\theta||$
　　　
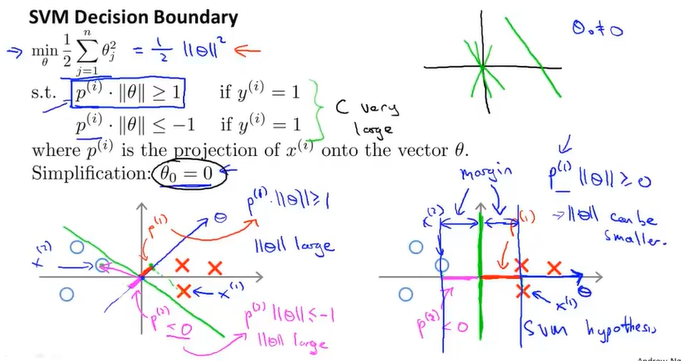
　　　目标函数是最小化theta，为什么这个公式是这样和以前不同，我觉得是因为支持向量机通过令X*theta大于1和小于-1的方法令前面那部分变成了0，所以只需要考虑后面那部分系数的影响。
　　　而为了使theta足够小的同时满足大于1和小于-1的条件，投影p需要足够的大，投影映射到图像上便是所谓的间距，这就是为什么支持向量机能够有大间距的性质。

12-4核函数

　　　核函数kernel function
　　　
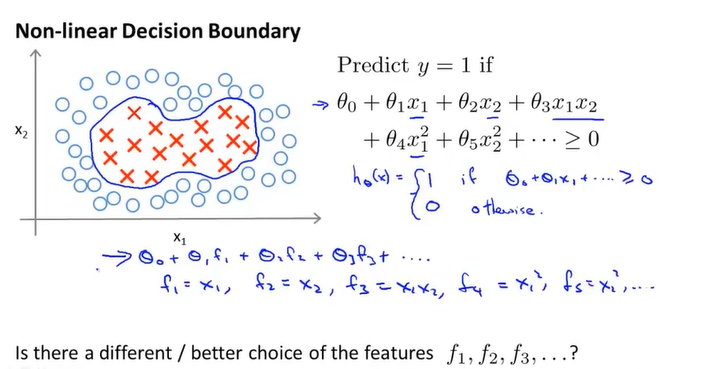
　　　高斯核函数
　　　
　　
　　　核函数和相似函数
　　　$$f_1 = similarity\left(x,l^{\left(1\right)}\right)=exp\left(-\frac{\sum_{j=1}^n{\left(x_j-l_j^{\left(1\right)}\right)^2}}{2\sigma^2}\right)$$

　　　如果x约等于$l^{\left(1\right)}$, 则f1会约等于1
　　　如果x和$l^{\left(1\right)}$相差很远，那么f1会约等于0

　　　
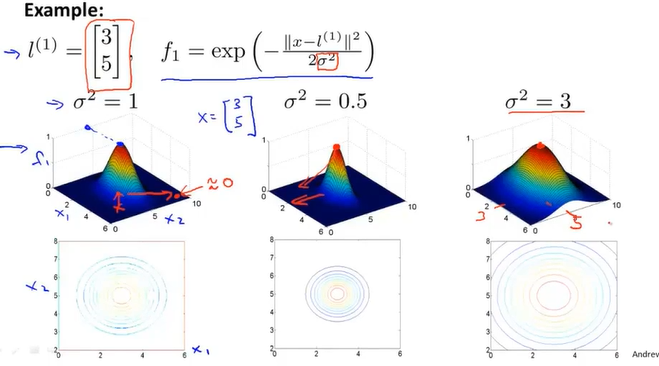
　　　sigma对函数图像的影响

　　　
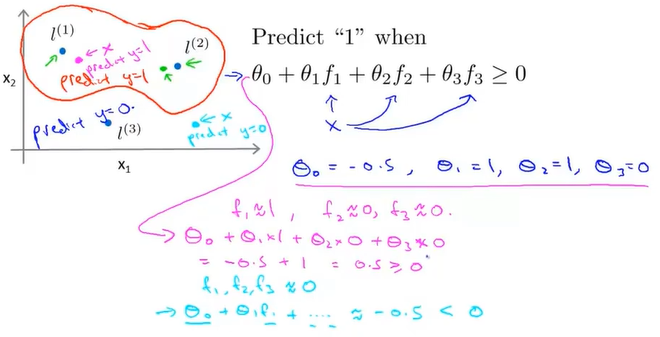
　　　核函数的做法即为，选定几个标记点landmark，则在某些标记点预测值为1的情况下，接近这些标记点的样本预测值便为1，远离则为0.

12-5核函数-补充

　　　
　　　标记点的选取，即把所有的样本点都当成标记点去计算

　　　
　　　这边讲解了训练的函数，在某些应用中，在进行正则化的时候会使用$\theta^TM\theta$,这里的M是一个特殊的矩阵，使用这个矩阵来正则化能够加快运算的速度

　　　在SVM的参数中，有C和sigma，两个参数对函数图像的影响如下
　　　

12-6使用SVM

　　　举例：线性核函数、高斯核函数、多项式核函数、字符串核函数、卡方核函数、直方相交核函数……
　　　在使用函数前进行特征归一化
　　　使用的核函数需要满足默塞尔定理

　　　根据样本数和特征数进行选择
　　　
　　　即当特征数小，样本数量适中时，才是用高斯核函数
　　　其他情况下，如特征数大，样本数量过小，或者特征数小，样本数量大的时候，通常去使用线性核函数或者线性回归

13-1无监督学习

无监督学习*unsupervised learning*: 样本点不提供标签
簇分配过程*cluster assignment step*

13-2K-means算法

聚类中心 cluster centroids

　　　过程：遍历所有的样本，根据与聚类中心的距离将所有的点分成两类。将两类的点计算均值，再将聚类中心移动到均值处的位置。
　　　算法过程如下:
　　　
　　　如果遇到没有点的聚类中心，正常是将其移除，如果需要K的簇，则再重新随机化一个值。