吴恩达机器学习Day11

13-3优化目标

　　　$c^{(i)}$表示样本$x^{(i)}$所属的聚类中心index
　　　$\mu_k$第k个均值中心的位置
　　　$\mu_c^{(i)}$表示$x^{(i)}$所属的聚类中心的位置
　　　如$x^{(i)}=5, c^{(i)}=5, so \; \mu_c^{(i)}=\mu_5 $
　　　优化目标函数，也叫失真代价函数(distortion cost function)
　　　
　　　K-均值算法
　　　初始化聚类中心的值
　　　弹幕提到这和物理上的旋转类似，旋转的最后结果总是会围绕某个轴。
　　　
　　　找出每个点所属的聚类中心的值也相当于最小化代价函数
　　　其次是根据均值找出各聚类中心的新位置

13-4随机初始化

　　　1. 聚类中心的数量必须小于样本量
　　　2. 随机选取K个训练样本
　　　3. 将这些训练样本作为聚类中心

　　　局部最优
　　　　　　
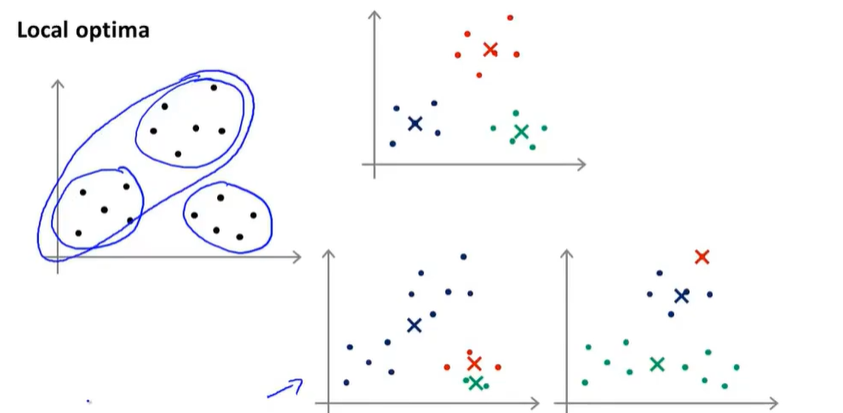
　　　做法
　　　　　　多次随机化聚类中心，运行算法，计算代价函数。

13-5选取聚类数量

肘部法则 the Elbow Method

　　　改变K的数量，计算各种情况的代价函数值
　　　
　　　如果和左图所示，图中有明显拐点，则拐点是较佳的K值，但如果右图没有明显拐点的就很难选出适合的K值

　　　查找什么K值适合后续目的
　　　如服装，需要分成大中小三种码数，则此时选择3种聚类中心是合适的。

14-1目标1——数据压缩

　　　维度压缩；减少类似的、无关紧要的特征。
　　　举例：将二维特征压缩为一维特征
　　　　　　

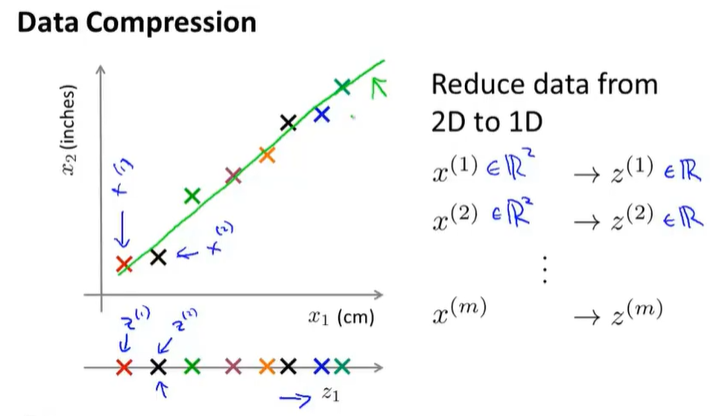
　　　将三维特征压缩为二维特征
　　　　　　将三维空间点投影到一个二维平面上
　　　　　　

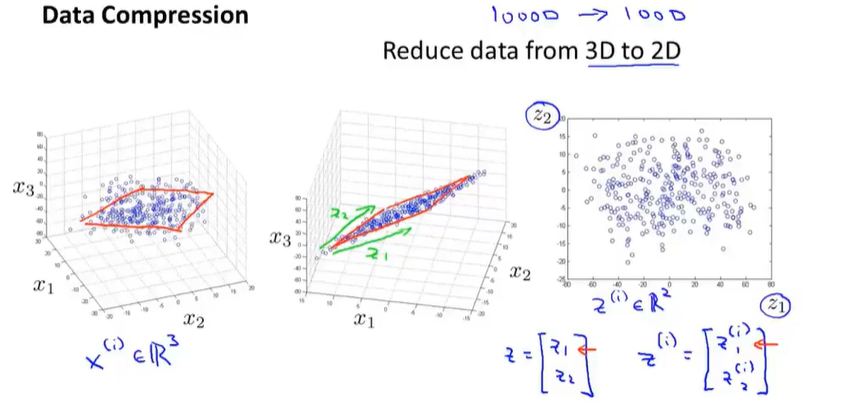
14-2目标2——可视化

　　　将大量的特征压缩为2-3个具有特征性的特征，然后画在图表上查看

14-3主成分分析问题规划1

Principal Component Analysis(PCA)

　　　PCA找到一个投影平面，在投影误差最小的前提下，将高维数据压缩为低维。

　　　将n维数据压缩到k维：找到k个向量$u^{(1)} \dots u^{(k)}$来投影这些样本点，最小化这个投影误差。

　　　尽管看上有些像素，但是PCA和线性回归不同，在PCA中计算的是投影误差（正交误差），而线性回归是垂直误差。

14-4主成分分析问题规划2

　　　1. 预处理：特征归一化和均值标准化
　　　2. 计算协方差covariance matrix
　　　$$\Sigma = \frac{1}{m}\sum_{i=1}^{n}{(x^{(i)}-\mu)(x^{(i)}-\mu)^T}$$
　　　(貌似图片给的公式有误)
　　　3. 计算协方差矩阵的特征向量
　　　$$[U,S,V] = svd(Sigma)$$
　　　
　　　U的前k个向量既是投影方向
　　　4. 用算出来的投影方向乘上X得到新的向量Z
　　　

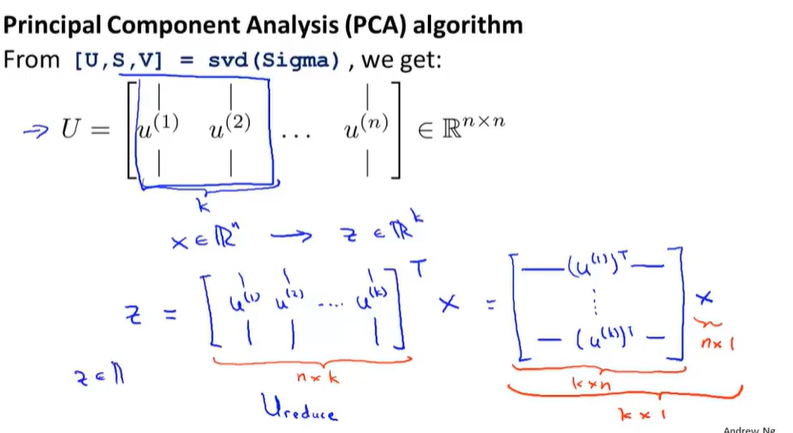
14-5主成分数量选择

　　　选择k：1. 平均平方投影误差
　　　　　　 2. 计算数据的总方差
　　　　　　 3. 选择最小的k使得下面是自≤0.01，即“99%的方差性得以保留”
　　　

选择k的算法

　　　
　　　这个S是一个n*n的矩阵，除了对角线之外其他元素都是0，可是不知道为什么用$$1-\frac{\sum_{i=1}^k{S_{ii}}}{\sum_{i=1}^n{S_{ii}}} \leq 0.01$$

14-6压缩重现

　　　
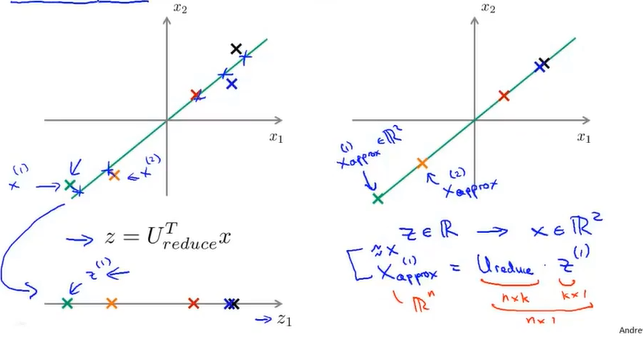
　　　$$X_approx^{(1)} = U_reduce · z^{(1)}$$

14-7应用PCA的建议

加速监督学习

错误使用PCA

　　　PCA不是防止过拟合的方式。PCA在不考虑y值的情况下舍弃掉了一些有用的信息，只是单纯保持了样本的方差。

　　　PCA并非一定要用，在应用PCA之前先使用原始数据，如果不能很好地拟合的话才会使用PCA算法。